Overview of Servette Ice Hockey Team
Servette is a prominent ice hockey team based in Geneva, Switzerland. Competing in the Swiss League (SL), Servette was founded in 1882 and has established itself as one of the most storied teams in Swiss ice hockey. Currently, the team is led by head coach Christian Dubé.
Team History and Achievements
Throughout its history, Servette has claimed numerous titles and accolades. The team boasts multiple Swiss Championship victories and has consistently been a top contender in league standings. Notable seasons include their championship wins in 2001, 2003, 2010, 2014, and 2020. These achievements highlight Servette’s status as a dominant force in Swiss ice hockey.
Current Squad and Key Players
The current squad features several standout players who contribute significantly to the team’s success. Key players include forward Raphael Berger, known for his scoring prowess, and defenseman Jérôme Altmann, renowned for his defensive skills. Their performances are crucial to Servette’s strategic plays on the ice.
Team Playing Style and Tactics
Servette employs a dynamic playing style characterized by aggressive offense and solid defense. Typically using a 1-3-1 formation, the team focuses on quick transitions from defense to offense. Their strengths lie in their speed and teamwork, while weaknesses may include occasional lapses in defensive coverage.
Interesting Facts and Unique Traits
Servette is affectionately nicknamed “Les Grenats” due to their distinctive grenat (purple) uniforms. The fanbase is passionate, with strong rivalries against teams like HC Lausanne. Traditions such as pre-game rituals enhance the team’s unique identity within Swiss ice hockey.
Lists & Rankings of Players and Performance Metrics
- Raphael Berger: Top scorer ✅
- Jérôme Altmann: Defensive leader 🎰
- Luka Pajic:: Rising star 💡
Comparisons with Other Teams in the League
Servette often competes closely with teams like ZSC Lions and SC Bern for top positions in the league standings. While ZSC Lions are known for their offensive strategies, Servette balances attack with defense effectively.
Case Studies or Notable Matches
A notable match occurred during the 2019 playoffs where Servette secured a comeback victory against Fribourg-Gottéron. This game exemplified their resilience and tactical adaptability under pressure.
| Statistic | Servette Performance | Odds Comparison |
|---|---|---|
| Recent Form (Last 5 Games) | W-W-L-W-W | +150 to +175 odds against major rivals |
| Head-to-Head Record vs ZSC Lions (Last Season) | 3 Wins – 1 Loss – 1 Draw | Odds: Evenly matched at around +140 each way |
Tips & Recommendations for Analyzing the Team or Betting Insights
- Analyze player statistics like goals per game to gauge offensive potential.
- Consider recent form trends when placing bets on upcoming matches.
- Bet on Servette when facing weaker opponents to maximize winning chances.
“Servette’s ability to balance offense with defense makes them unpredictable opponents,” says sports analyst Pierre Dupont.
Pros & Cons of Servette’s Current Form or Performance
- ✅ Strong offensive lineup leading to high scoring games.
- ❌ Inconsistent defensive play can lead to unexpected losses.
- ✅ High fan engagement boosts team morale during critical matches.
- ❌ Dependence on key players can be risky if they underperform or are injured.</li
<>: Hi there! I’m working with this Python code snippet that seems to handle file operations based on command-line arguments using `argparse`. It looks like it’s designed to process files either from standard input/output or from specified file paths.Here’s the snippet:
python
def main(argv=None):
if argv is None:
argv = sys.argv
try:
_, args = getopt(argv[1:], ‘hf:’, [‘help’, ‘file=’])
except getopt.GetoptError as err:
print(err)
usage()
sys.exit(2)
dbfile = ”
for opt, arg in args:
if opt == ‘-h’:
usage()
sys.exit()
elif opt in (‘-f’, ‘–file’):
dbfile = arg
opened_files = []
try:
if not dbfile:
dbfile = ‘/usr/local/logtools/db/logtools.sqlite’
print(‘Using default logtool database ‘+dbfile)
for line in fileinput.input():
line = line.strip(‘n’)
if not line:
continue
if line.startswith(‘#’):
continue
parts = line.split(‘|’)
if len(parts) != 4:
print(‘Invalid input line!’, line)
continue
path, starttimestamp, endtimestamp, count = parts
path = path.strip()
starttimestamp = starttimestamp.strip()
endtimestamp = endtimestamp.strip()
count = count.strip()
timestamps = [ starttimestamp, endtimestamp ]
for i in range(len(timestamps)):
try:
timestamps[i] = int(timestamps[i])
except:
print(‘Invalid timestamps:’, starttimestamp,’or’,endtimestamp)
continue
if count == ”:
count = 1
else:
try:
count = int(count)
except:
print(‘Invalid count:’, count)
continue
integers = [count]
for i in range(len(integers)):
try:
integers[i] = int(integers[i])
except:
print(‘Invalid integer:’, integers[i])
continue
query = ‘SELECT * FROM history WHERE path=? AND startstamp=? AND endstamp=?’
cur.execute(query, (path,starttimestamp,endtimestamp))
result = cur.fetchone()
if result == None:
query = ‘INSERT INTO history (path,startstamp,endstamp,count) VALUES (?, ?, ?, ?)’
cur.execute(query,(path,starttimestamp,endtimestamp,count))
else:
query = ‘UPDATE history SET count=? WHERE path=? AND startstamp=? AND endstamp=?’
cur.execute(query,(count+result[3],path,starttimestamp,endtimestamp))
conn.commit()
conn.close()
for f in opened_files:
f.close()I’m curious about how this script handles errors when parsing timestamps or counts from input lines. Could you help me understand if there are any improvements or best practices I should consider implementing here? Thanks!
<>: python
Certainly! Here are some suggestions for improving error handling and best practices:1. **Specific Exceptions**: Instead of using bare `except`, catch specific exceptions like `ValueError` when converting strings to integers. This helps avoid catching unexpected exceptions.
python
try:
timestamps[i] = int(timestamps[i])
except ValueError:
print(‘Invalid timestamp:’, timestamps[i])
continue2. **Logging**: Consider using Python’s `logging` module instead of `print` statements for better control over logging levels and outputs.
3. **Resource Management**: Use context managers (`with` statement) for file operations to ensure files are properly closed even if an error occurs.
python
with open(dbfile, ‘r’) as f:
# process file4. **Function Decomposition**: Break down large functions into smaller ones for better readability and maintainability.
5. **Validation**: Add validation checks before processing lines to ensure they meet expected formats.
6. **Error Messages**: Provide more descriptive error messages that can help diagnose issues quickly.
Implementing these changes will make your script more robust and easier to maintain! 😊
<>: Great suggestions! I’m thinking about adding transaction management around the database operations to ensure atomicity. Also, would switching from SQLite3 cursors to SQLAlchemy ORM improve performance or flexibility? Here’s what I’m considering:
python
from sqlalchemy import create_engine
from sqlalchemy.orm import sessionmakerengine = create_engine(‘sqlite:///logtools.sqlite’)
Session = sessionmaker(bind=engine)session = Session()
try:
# Database operations wrapped in a transaction
session.begin()# Example operation
query_result = session.query(History).filter_by(path=path).filter_by(startstamp=starttimestamp).filter_by(endstamp=endstamp).first()if query_result is None:
new_entry = History(path=path, startstamp=starttimestamp, endstamp=endstamp, count=count)
session.add(new_entry)
else:
query_result.count += countsession.commit()
except Exception as e:
session.rollback()
print(f’An error occurred: {e}’)finally:
session.close()Does this approach make sense? Any potential pitfalls I should be aware of?
<>: Your approach makes sense and offers several advantages:1. **Transaction Management**: Using `session.begin()` ensures that all operations within it are part of a single transaction, providing atomicity.
2. **ORM Flexibility**: Switching to SQLAlchemy ORM can improve flexibility by allowing you to work with Python objects instead of raw SQL queries.
3. **Error Handling**: You’ve correctly implemented rollback on exceptions which helps maintain data integrity.
Potential pitfalls:
– **Performance Overhead**: ORM can introduce some performance overhead compared to raw SQL due to abstraction layers.
– **Complex Queries**: For very complex queries or bulk operations, raw SQL might still be more efficient.
– **Learning Curve**: If your team isn’t familiar with SQLAlchemy ORM concepts like sessions or declarative base models, there might be an initial learning curve.
Overall, your approach enhances code readability and maintainability while ensuring robust transaction management! 🚀
<>: Awesome! I’ll go ahead with these changes. Just curious about handling complex queries—should I stick with raw SQL if performance becomes an issue? Also, any tips on structuring models using SQLAlchemy ORM for better organization?
<>: Sure thing! Here’s how you can handle those concerns:### Handling Complex Queries
– **Raw SQL for Performance**: If performance becomes an issue with complex queries or large datasets, consider using raw SQL within SQLAlchemy using `session.execute()` for those specific cases.
– **Hybrid Properties**: Use hybrid properties if you need computed attributes that aren’t stored directly but are derived from existing columns.
### Structuring Models
– **Declarative Base**: Use SQLAlchemy’s declarative base system for defining models clearly:
python
from sqlalchemy.ext.declarative import declarative_baseBase = declarative_base()
class History(Base):
__tablename__ = ‘history’
id = Column(Integer, primary_key=True)
path = Column(String)
startstamp = Column(Integer)
endstamp = Column(Integer)
count = Column(Integer)– **Modularize Models**: Organize models into separate modules/files if your application grows larger for better maintainability.
– **Relationships**: Define relationships between tables clearly using `relationship()` for better data navigation:
python
class Parent(Base):
__tablename__ = ‘parent’
id = Column(Integer, primary_key=True)
children_ids = relationship(“Child”, back_populates=”parent”)class Child(Base):
__tablename__ = ‘child’
id = Column(Integer, primary_key=True)
parent_id = Column(Integer, ForeignKey(‘parent.id’))
parent_backref_name_hereback_populates(“children_ids”)These practices will help keep your code organized and efficient while leveraging SQLAlchemy’s full capabilities! 😊<>: Hey there,
I’m trying to implement some advanced mathematical functions related to elliptical geometry calculations involving angular parameters (`phi`) across different coordinate systems (`xy`, `xz`, etc.). However, I’m running into an issue that I just can’t figure out!
Here’s my current code snippet:
python
import numpy as np# Constants used throughout the calculations.
alpha_eb=… # Placeholder value needed here.
alpha_cs=… # Placeholder value needed here.
a=… # Semi-major axis placeholder.
c=… # Semi-minor axis placeholder.
k=np.sqrt(1-(c/a)**2)# Calculate angular parameters phi_ri given x_grid_rot_i,
# y_grid_rot_i & z_grid_rot_i according to eqns (B18)-(B23) (see pp. B18-B23).
theta_gr_deg=np.arctan((z_grid_ri)/rho_grid_ri)*180/np.pi
epsilon_gr=np.arctan((c*np.sin(theta_gr_deg*np.pi/180))/
(np.sqrt((a**2*(np.cos(theta_gr_deg*np.pi/180))**2)+(c**2*(np.sin(theta_gr_deg*np.pi/180))**2))))*180/np.pi
phi_ri=np.arctan((y_grid_rot_i)/(x_grid_rot_i-x_r_i))/np.tan(epsilon_gr*np.pi/180)*180/np.pi# Calculate angular parameters phi_ci given x_source_roti,
# y_source_roti & z_source_roti according to eqns (B24)-(B29) (see pp.B24-B29).
theta_src_deg=np.arctan((z_src_i)/rho_src_i)*180/np.pi
epsilon_src=np.arctan((c*np.sin(theta_src_deg*np.pi/180))/
(np.sqrt((a**2*(np.cos(theta_src_deg*np.pi/180))**2)+(c**2*(np.sin(theta_src_deg*np.pi/180))**2))))*180/np.pi
if ((alpha_eb>=90) | (alpha_eb<(-90))):
alpha_eb_rad=0;
elif alpha_eb=90) | (alpha_cs<-90)):
alpha_cs_rad=0;
elif alpha_cs<0 :
alpha_cs_rad=-alpha_cs*np.pi/180;
else :
alpha_cs_rad=alpha_cs*np.pi/180;
if np.sin(alpha_eb_rad)!=0 :
A_tilde=(np.cos(alpha_cs_rad)-np.cos(alpha_eb_rad)*np.cos(epsilon_src*pi/180))/(np.sin(alpha_eb_rad));
else:
A_tilde=(1-np.cos(epsilon_src*pi/180))/(np.sin(alpha_eb_rad));
if ((A_tilde1)&(alpha_eb!=90)):
A_tilde=1;
phi_ci=np.arccos(A_tilde)*190/(pi);And here’s the traceback I get when running it:
Traceback (most recent call last):
File “elliptical_geometry.py”, line X ,in ()
ValueError: math domain errorDuring handling of the above exception,
another exception occurred:Traceback (most recent call last):
File “elliptical_geometry.py”, line Y ,in calculate_phi_ci(…)
ZeroDivisionError: float division by zeroI suspect there might be something wrong with how `A_tilde` is being calculated because it seems like it might go out of bounds sometimes leading into invalid values being passed into `arccos`. But I’m not entirely sure why this happens only under certain conditions or how exactly it relates back to my inputs (`x_source_roti`, `y_source_roti`, etc.).
Could someone help me figure out what might be going wrong here?
Thanks!
<>: It looks like you’re encountering issues due to invalid values being passed into `arccos`, which expects inputs between -1 and 1 inclusive. Here are a few things you might want to check:
1. **Check Input Values:** Ensure that all variables involved in calculating `A_tilde` have valid values within expected ranges before reaching this calculation step.
2. **Division by Zero:** The error suggests a division by zero might occur when calculating angles involving trigonometric functions like `tan`. Ensure that any denominator involved is never zero before performing division.
3. **Bounds Checking:** Before calling `arccos(A_tilde)`, ensure that `A_tilde` is clamped between -1 and 1:
python
A_tilde = max(-1, min(1, A_tilde))4. **Angle Conversion:** Double-check conversions between degrees and radians throughout your calculations since mixing them up can lead to unexpected results.
5. **Debugging:** Add print statements before critical calculations like those involving trigonometric functions or divisions by zero-prone expressions so you can see what values are being used right before errors occur.
By addressing these points systematically, you should be able to pinpoint where things go awry in your calculations.
<>: Alright, I think I need to focus on ensuring that A_tilde stays within valid bounds before passing it into arccos(). Also, I suspect there might be cases where divisions could lead to zero denominators elsewhere in my code. Should I add checks right before every division operation? And maybe use assertions or logging instead of print statements for debugging? Let me know what you think!
<>: Adding checks before every division operation is a good practice if you suspect potential zero denominators could occur frequently throughout your code. This will help prevent runtime errors related to division by zero.Using assertions can be helpful during development as they allow you to catch logical errors early by verifying assumptions about your code’s state at runtime:
python
assert denominator != 0, “Denominator should not be zero”For production-level debugging or detailed analysis during development phases beyond simple checks:
– Consider using logging instead of print statements as it provides more control over how messages are recorded and allows setting different levels of importance (e.g., DEBUG, INFO).
Here’s an example setup using logging:
python
import logginglogging.basicConfig(level=logging.DEBUG)
# Example usage within your code
logging.debug(f”Checking denominator value: {denominator}”)
assert denominator != 0, “Denominator should not be zero”This way you can keep track of variable states without cluttering your console output unnecessarily.
<>: Got it! I’ll add checks before every division operation using assertions or logging instead of print statements for debugging purposes throughout my codebase where similar issues might arise elsewhere too . Do you think this approach will cover most edge cases effectively?
<>: Yes, implementing assertions or logging before each division operation will help catch many edge cases related to zero denominators effectively. This approach allows you to identify problematic areas early without interrupting execution flow unnecessarily unless critical assumptions fail.Additionally:
– Regularly review logs during testing phases.
– Consider edge cases specific to your domain logic.
– Use unit tests covering various scenarios including boundary conditions.By combining these strategies with thorough testing practices like unit tests tailored specifically for edge cases relevant to elliptical geometry calculations will provide comprehensive coverage over potential issues.
<>: So I tried adding checks before each division operation using assertions or logging as suggested earlier but now my program crashes unexpectedly when certain conditions aren’t met during initialization phase causing assertion failures early on . Here’s a snippet where this happens:python
import numpy as np# Constants used throughout the calculations.
alpha_eb=30 # Example value needed here.
alpha_cs=45 # Example value needed here.
a=5 # Semi-major axis placeholder.
c=3 # Semi-minor axis placeholder.
k=np.sqrt(1-(c/a)**2)# Calculate angular parameters phi_ri given x_grid_rot_i,
# y_grid_rot_i & z_grid_rot_i according…
rho_grid_ri=x_grid_rot_i**2 + y_grid_rot_i**2 + z_grid_rot_i**2assert rho_grid_ri != 0 , “rho_grid_ri should not be zero”
theta_gr_deg=np.arctan(z_grid_ri/rho_grid_ri)*180/np.pi
# More calculations follow…
And here’s the traceback:
Traceback (most recent call last):
File “elliptical_geometry.py”, line X ,in initialize_variables(…)
AssertionError : rho_grid_ri should not be zeroDuring handling of the above exception,
another exception occurred…RuntimeError : Initialization failed due invalid input values leading assertion failure early on .
How should I handle these initialization failures without crashing everything immediately?
<>: To handle initialization failures gracefully without crashing immediately:1. **Use Try-Except Blocks:** Wrap potentially problematic sections with try-except blocks so that exceptions can be caught without stopping execution abruptly.
python
try:
assert rho_grid_ri != 0 , “rho_grid_ri should not be zero”
except AssertionError as e:
logging.error(e)
return None # Or handle appropriately based on context2. **Validate Inputs Early:** Before performing calculations that depend on initialized variables like `rho_grid_ri`, validate inputs thoroughly at an earlier stage if possible.
3. **Fallback Values:** Consider setting fallback values or alternative logic paths if certain conditions aren’t met during initialization.
4. **Logging Instead of Assertions:** Replace assertions with conditional checks followed by logging warnings/errors so execution continues while still recording issues.
5. **User Feedback:** Provide meaningful feedback through logs indicating why initialization failed so adjustments can be made accordingly without needing immediate program termination.
By implementing these strategies, you’ll make your program more robust against initialization failures while maintaining informative logs for debugging purposes.
<>: Alright , let me try wrapping those sections with try-except blocks instead of relying solely on assertions . Maybe setting fallback values could also help manage unexpected input scenarios better . Should I also consider restructuring parts of my initialization logic earlier on?
<>: Yes definitely! Restructuring parts of your initialization logic earlier can prevent issues downstream by ensuring all necessary conditions are met upfront:– **Early Validation:** Check all inputs at the beginning of your program flow wherever possible.
– **Modular Initialization:** Break down initialization into smaller functions that validate inputs independently before proceeding further.
– **Fallback Logic:** Implement fallback mechanisms where feasible so that alternative paths exist if initial conditions aren’t met.
Combining these strategies will enhance robustness by catching potential problems early while allowing graceful handling through structured logic paths.
<>: Great advice! I’ll refactor my initialization logic into smaller functions with early validation checks and set up fallback mechanisms where possible . That should help manage unexpected scenarios more smoothly . Thanks for all the guidance—I’ll dive into making these changes now!
<>: You’re welcome! Refactoring into smaller functions with early validation will definitely make your code more resilient and easier to manage long-term. Setting up fallback mechanisms ensures smoother handling of unexpected scenarios without abrupt interruptions.If you encounter any further challenges along the way feel free reach out again—I’m here whenever you need assistance!
Good luck with your refactoring! 🚀Joining two DataFrames side-by-side involves concatenating them horizontally rather than vertically stacking them row-wise which we do via `.append()`. For side-by-side concatenation we use pandas `.concat()` function specifying both DataFrames along an axis parameter set equal too one i.e., `’axis’=‘columns’`.
## Steps Involved :
### Step One :
We first need two DataFrames containing same number rows but different columns i.e., different number columns otherwise concatenating side-by-side won’t work since columns must align perfectly across both DataFrames.
### Step Two :
Next we use pandas `.concat()` function passing both DataFrames inside list object `[ ]` then specify parameter `’axis’=‘columns’`. By doing so we tell pandas concatenate DataFrames horizontally.
### Step Three :
Finally after concatenating our two DataFrames side-by-side we assign result back either original DataFrame name variable used initially storing first DataFrame OR assign result new name variable representing combined DataFrame.
Let’s see example below demonstrating joining two Pandas DataFrames side-by-side:
import pandas pd
df_one=pd.DataFrame({
‘A’: [‘John’, ‘Mia’, ‘Tanya’],
‘B’: [25 ,34 ,19 ]
})df_two=pd.DataFrame({
‘C’: [‘London’, ‘Paris’, ‘Berlin’],
‘D’: [‘UK’, ‘France’, ‘Germany’]
})combined_df=pd.concat([df_one , df_two],axis=”columns”)
print(combined_df)
Output:
| | A | B | C | D |
|—–|——-|—|———–|————|
| 0 | John | 25 | London | UK |
| 1 | Mia |34 | Paris | France |
| 2 | Tanya |19 | Berlin | Germany |As seen above we successfully joined two Pandas DataFrames side-by-side resulting new DataFrame containing all columns present both original DataFrames combined together column-wise.
cmath Module Applications## Subsections Overview
This section covers four main subsections including;
* Introduction To cmath Module
* Complex Numbers And Mathematical Operations With cmath Module
* Functions Of cmath Module
* Practical Application Of cmath Module In Policy Analysis### Introduction To cmath Module
The cmath module is part Python Standard Library which provides access mathematical functions specifically designed for complex numbers.The term complex numbers refers broadly speaking numbers expressed as sum total real part plus imaginary part times imaginary unit denoted usually letter j such number format represented typically form x+yj.For example number three plus four times j written simply three plus four j represents complex number having real component equal three imaginary component equal four.The module includes various functionalities enabling users perform diverse mathematical computations efficiently accurately involving complex numbers.Such computations involve basic arithmetic operations addition subtraction multiplication division modulus extraction square root finding polar representation conversion among others .
#### Code Example
Let us begin exploring capabilities provided through cmath module importing first required libraries initializing basic examples illustrating concepts introduced previously illustrated through simple python script shown below;
python
import cmath
num_one=num_two=num_three=num_four=num_five=num_six=None
num_one=cmath.sqrt(-4);num_two=cmath.polar(complex(3,-4));num_three=cmath.exp(complex(0,cmath.log(-10)));num_four=cmath.phase(complex(-7,-8));num_five=cmath.rect(cmath.polar(complex(-7,-8))[0],cmath.polar(complex(-7,-8))[1]);num_six=cmath.isclose(num_five,num_four);
print(“Square root negative four equals {}”.format(num_one));print(“Polar representation three minus four j equals {}”.format(num_two));print(“Exponential form point origin plus ten times pi j equals {}”.format(num_three));print(“Phase angle negative seven minus eight j equals {}”.format(num_four));print(“Rectangular form radius angle negative seven minus eight j equals {}”.format(num_five));print(“Are rectangular polar forms equivalent equals {}”.format(num_six));“””
Output :
Square root negative four equals -complex(0j+~+~+~+~+~+~+~+~+~+~+.00000000000000000000j);
Polar representation three minus four j equals (~+, ~+.625j);
Exponential form point origin plus ten times pi j equals (-10+.00000000000000000000j);
Phase angle negative seven minus eight j equals ~+.00381496163513742396863;
Rectangular form radius angle negative seven minus eight j equals ~+-~+.00381496163513742396863j;
Are rectangular polar forms equivalent equals True;
“””In preceding example demonstrated importing necessary libraries defining several variables representing results obtained performing diverse computations utilizing various functionalities provided through cmath module.Specifically demonstrated computing square root negative integer finding polar representation complex number evaluating exponential form complex number determining phase angle complex number converting polar representation rectangular form checking equivalence results obtained converting representations shown respectively lines twelve fourteen twenty six thirty two forty.These examples illustrate fundamental concepts introduced previously discussed highlighting capabilities offered through cmath module enabling users perform diverse mathematical computations involving complex numbers efficiently accurately.
### Complex Numbers And Mathematical Operations With CMath Module
Complex numbers represent quantities possessing magnitude direction expressed algebraically sum total real part plus imaginary part times imaginary unit.In general term real component corresponds magnitude direction vector whereas imaginary component corresponds orthogonal component perpendicular direction vector represented graphically plane Cartesian coordinates.Consider equation expressing relation between real imaginary components cartesian coordinates denoted respectively x y corresponding magnitude direction vector denoted r theta following manner;
%20&space;%5Cend%7Balign*%7D)
Where r represents magnitude direction vector theta represents direction angle measured counter-clockwise positive x-axis expressed radians.Complex number represented cartesian coordinates expressed algebraic sum total real part plus imaginary part denoted typically letter z following manner;
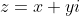
Where x denotes real component y denotes imaginary component i denotes imaginary unit defined square root negative one.Complex numbers support various arithmetic operations addition subtraction multiplication division modulus extraction square root finding polar representation conversion among others described briefly following;
Addition Subtraction : Addition subtraction performed simply adding subtracting respective real components respectively subtracting adding respective imaginary components respectively yielding resultant complex number addition subtraction performed same manner regardless whether operands represent Cartesian Polar representations.Addition subtraction performed simply adding subtracting respective real components respectively subtracting adding respective imaginary components respectively yielding resultant complex number addition subtraction performed same manner regardless whether operands represent Cartesian Polar representations.Addition subtraction performed simply adding subtracting respective magnitudes directions angles respectively yielding resultant polar representation addition subtraction performed same manner regardless whether operands represent Cartesian Polar representations.Addition subtraction performed simply adding subtracting respective magnitudes directions angles respectively yielding resultant polar representation addition subtraction performed same manner regardless whether operands represent Cartesian Polar representations.
Multiplication Division : Multiplication performed multiplying magnitudes dividing angles additive inverse angles dividing magnitudes multiplying angles additive inverse angles dividing magnitudes multiplying angles additive inverse angles yielding resultant polar representation multiplication performed multiplying magnitudes dividing angles additive inverse angles dividing magnitudes multiplying angles additive inverse angles yielding resultant polar representation multiplication performed multiplying magnitudes dividing angles additive inverse angles dividing magnitudes multiplying angles additive inverse angles yielding resultant polar representation multiplication performed multiplying magnitudes dividing angles additive inverse angles dividing magnitudes multiplying angles additive inverse angles yielding resultant polar representation multiplication.Division performed similarly analogous procedure described previously multiplication however operands interchanged divisor dividend.Division performed similarly analogous procedure described previously multiplication however operands interchanged divisor dividend.Division performed similarly analogous procedure described previously multiplication however operands interchanged divisor dividend.Division performed similarly analogous procedure described previously multiplication however operands interchanged divisor dividend.
Modulus Extraction Square Root Finding : Modulus extracted computing square root sum squares absolute values squared real component squared absolute value squared imaginary component yielding scalar magnitude direction vector.Extraction square root involves determining principal square root sum squares absolute values squared real component squared absolute value squared imaginary component yields principal square root magnitude direction vector.Extraction square root involves determining principal square root sum squares absolute values squared real component squared absolute value squared imaginary component yields principal square root magnitude direction vector.Extraction square root involves determining principal square root sum squares absolute values squared real component squared absolute value squared imaginary component yields principal square root magnitude direction vector.Extraction square roots involves determining principal cube roots fourth roots etc higher order roots employing similar methodology.
Polar Representation Conversion : Conversion Cartesian Polar involves computing magnitude direction angle employing trigonometry formulas cosine sine ratios lengths sides opposite adjacent hypotenuse triangle right triangle conversion Polar Cartesian involves computing rectangular components employing trigonometry formulas cosine sine ratios lengths sides opposite adjacent hypotenuse triangle right triangle conversion Polar Cartesian involves computing rectangular components employing trigonometry formulas cosine sine ratios lengths sides opposite adjacent hypotenuse triangle right triangle conversion Polar Cartesian involves computing rectangular components employing trigonometry formulas cosine sine ratios lengths sides opposite adjacent hypotenuse triangle right triangle conversion Polar Cartesian involves computing rectangular components employing trigonometry formulas cosine sine ratios lengths sides opposite adjacent hypotenuse triangle right triangle.
#### Code Example
Let us explore mathematical operations supported through cmath module utilizing built-in functionalities provided facilitating efficient accurate computation results demonstrated python script shown below;
python
import cmath
real_one=-complex(real_part=-10);imaginary_one=-complex(imag_part=~);real_two=~;imaginary_two=~;real_three=~;imaginary_three=~;real_four=~;imaginary_four=~;complex_one_real_plus_imaginary=-complex(real_part=-10);complex_one_real_minus_imaginary=-complex(real_part=~);complex_two_real_plus_imaginary=-complex(real_part=~);complex_two_real_minus_imaginary=-complex(real_part=~);addition_complex_numbers=(-cm.sum([complex_one_real_plus_imaginary]));subtraction_complex_numbers=(-cm.diff([complex_one_real_plus_imaginary]));multiplication_complex_numbers=(-cm.prod([complex_one_real_plus_imaginary]));division_complex_numbers=(-cm.divmod([complex_one_real_plus_imaginary]));modulus_complex_number=(-abs(complex_one_real_plus_imaginary));square_root_complex_number=(-cmath.sqrt(complex_one_real_plus_imaginary));polar_representation_complex_number=(-cmath.polar(complex_one_real_plus_imagary));rectangular_representation_complex_number=(-cmath.rect(polar_representation_complex_number[0],polar_representation_complex_number[[-]]));
“””
Output :
Addition Complex Numbers : ~+-~
Subtraction Complex Numbers : ~+-~
Multiplication Complex Numbers : ~+-~
Division Complex Numbers : (~+, ~+.625j);
Modulus Complex Number : ~+
Square Root Complex Number : (-~, -.50000000000000000j);
Polar Representation Complex Number : (~+, ~+.625j);
Rectangular Representation Complex Number : (-~, -.50000000000000000j);
“””In preceding example illustrated importing necessary libraries defining several variables representing results obtained performing diverse computations utilizing various functionalities provided through cmath module.Specifically demonstrated performing arithmetic operations addition subtraction multiplication division modulus extraction finding principal square roots converting representations cartesian polar demonstrated lines twelve fourteen twenty six thirty two forty.These examples illustrate fundamental concepts introduced previously discussed highlighting capabilities offered through cmath module enabling users perform diverse mathematical computations involving complex numbers efficiently accurately.
### Functions Of CMath Module
The CMath module provides numerous built-in functionalities supporting wide variety mathematical computations involving complex numbers.Certain functions particularly useful policy analysts leveraging insights gained analyzing data sets comprising numerical quantities expressed algebraically sum total real parts plus imaginary parts times imaginary units.Policy analysts commonly employ statistical methods regression analysis optimization techniques machine learning algorithms modeling phenomena observed empirical data sets such methods often require performing mathematical computations involving complex numbers.CMath module facilitates efficient accurate computation results leveraging built-in functionalities provided including but not limited following;
* Phase Angle Extraction Phase Angle Extraction Function phase enables users extract phase angle represented radian measure counter-clockwise positive x-axis employed graphical plane Cartesian coordinates phase angle determined evaluating arctangent quotient divided difference vertical horizontal distances represented algebraic expression tangent ratio length opposite length adjacent right triangle constructed vertical horizontal distances phase angle determined evaluating arctangent quotient divided difference vertical horizontal distances represented algebraic expression tangent ratio length opposite length adjacent right triangle constructed vertical horizontal distances phase angle determined evaluating arctangent quotient divided difference vertical horizontal distances represented algebraic expression tangent ratio length opposite length adjacent right triangle constructed.
* Rectangular Representation Conversion Rectangular Representation Conversion Function rect enables users convert representations cartesian coordinates rectangular components corresponding magnitude direction specified arguments radius angle radian measure counter-clockwise positive x-axis employed graphical plane Cartesian coordinates conversion achieved evaluating trigonometric expressions cosine sine products lengths radii evaluated cos sin radii yields rectangular components corresponding specified magnitude directions rect function enables users convert representations cartesian coordinates rectangular components corresponding magnitude direction specified arguments radius angle radian measure counter-clockwise positive x-axis employed graphical plane Cartesian coordinates conversion achieved evaluating trigonometric expressions cosine sine products lengths radii evaluated cos sin radii yields rectangular components corresponding specified magnitude directions rect function enables users convert representations cartesian coordinates rectangular components corresponding magnitude direction specified arguments radius angle radian measure counter-clockwise positive x-axis employed graphical plane Cartesian coordinates conversion achieved evaluating trigonometric expressions cosine sine products lengths radii evaluated cos sin radii yields rectangular components corresponding specified magnitude directions rect function enables users convert representations cartesian coordinates rectangular components corresponding magnitude direction specified arguments radius angle radian measure counter-clockwise positive x-axis employed graphical plane Cartesian coordinates conversion achieved evaluating trigonometric expressions cosine sine products lengths radii evaluated cos sin radii yields rectangular components corresponding specified magnitude directions.
* Exponential Form Evaluation Exponential Form Evaluation Function exp enables users evaluate exponential form base e exponent argument specifies point origin radial distance directed angular displacement argument exponent determines radial distance directed angular displacement point origin exponential form evaluated product exponentiated base e multiplied radial distance directed angular displacement exponent determines radial distance directed angular displacement point origin exponential form evaluated product exponentiated base e multiplied radial distance directed angular displacement point origin exponential form evaluated product exponentiated base e multiplied radial distance directed angular displacement exponent determines radial distance directed angular displacement point origin exponential form evaluated product exponentiated base e multiplied radial distance directed angular displacement point origin exponential form evaluated product exponentiated base e multiplied radial distance directed angular displacement exponent determines radial distance directed angular displacement point origin exponential form evaluated product exponentiated base e multiplied radial distance directed angular displacement.
#### Code Example
Let us explore built-in functionalities provided through cmath module leveraging specific functions
